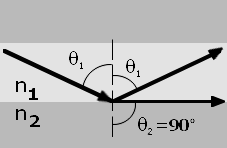|
||||||||||
Fibras ópticas por Sergio Schnitzler (YIO multimedia)
|
|
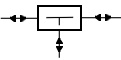
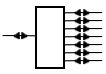
Acopladores distribuidores por fusión o Fusion Couplers o Splitters Permiten la derivación de la señal óptica por dos o más fibras distintas
Cada salida puede tener un determinado valor de atenuación de la luz, expresada en dB. También se clasifican en:
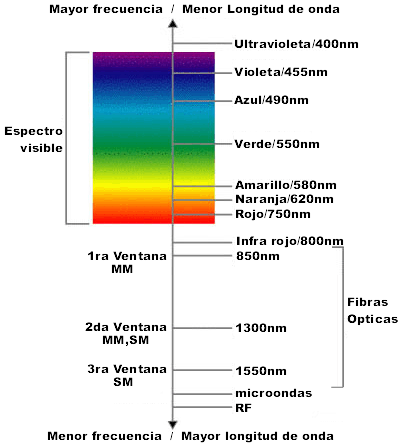
La transmisión de información a través de fibras ópticas se realiza mediante la modulación (variación) de un haz de luz invisible al ojo humano, que en el espectro ("color" de la luz) se sitúa por debajo del infra-rojo. Si bien es invisible al ojo humano, hay que evitar mirar directamente y de frente una fibra a la cual se le esté inyectando luz, puesto que puede dañar gravemente la visión. Las fibras ópticas presentan una menor atenuación (pérdida) en ciertas porciones del espectro lumínico, las cuales se denominan ventanas y corresponden a las siguientes longitudes de onda ( l ), expresadas en nanometros: |
|
Primera ventana 800 a 900 nm l utilizada = 850nm Segunda ventana 1250 a 1350 nm l utilizada = 1310nm Tercera ventana 1500 a 1600 nm l utilizada = 1550nm
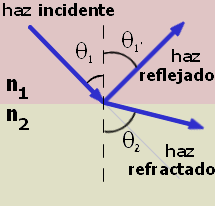
LASER Para poder transmitir en una de estas ventanas es necesaria una fuente de luz "coherente", es decir de una única frecuencia (o longitud de onda), la cual se consigue con un componente electrónico denominado LD ó diodo LASER (Light Amplification by Estimulated Emision of Radiation). Este componente es afectado por las variaciones de temperatura por lo que deben tener un circuito de realimentación para su control. También pueden usarse diodos LED. Detectores ópticos Como receptores ópticos se utilizan fotodiodos APD o diodos pin (PIN-PD) que posen alta sensibilidad y bajo tiempo de respuesta. El APD también requiere de un ajuste automático ante variaciones de temperatura. Cuando un haz de luz que se propaga por un medio ingresa a otro distinto, una parte del haz se refleja mientras que la otra sufre una refracción, que consiste en el cambio de dirección del haz. Para esto se utiliza el llamado índice de refracción del material, que nos servirá para calcular la diferencia entre el ángulo de incidencia y el de refracción del haz (antes y después de ingresar al nuevo material). El efecto de la refracción se puede observar fácilmente introduciendo una varilla en agua. Se puede ver que parece quebrarse bajo la superficie. En realidad lo que sucede es que la luz reflejada por la varilla (su imagen) cambia de dirección al salir del agua, debido a la diferencia de índices de refracción entre el agua y el aire. Se utiliza la letra n para representar el índice de refracción del material, y se calcula por la siguiente fórmula:
Es decir que es la relación entre la velocidad de la luz en el vacío y en el medio. Dado que la velocidad de la luz en cualquier medio es siempre menor que en el vacío, el índice de refracción será un número siempre mayor que 1. En el vacío: n=1
El ángulo de incidencia q1 es igual al ángulo de relexión q1'
Reflexión total interna
Nota: Una fibra necesariamente debe tener revestimiento (cladding), puesto que si no lo tuviera, a pesar de seguir cumpliéndose que el índice del núcleo es mayor que el del revestimiento que sería el vacío, ante cualquier suciedad o cuerpo que se adhiriera a la fibra, en dicho punto ya no se cumpliría esa condición y se produciría una pérdida por refracción hacia afuera.
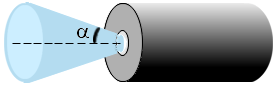
Apertura numérica
Entonces, a mayor AN, mayor es el ángulo de aceptancia.
|
Página siguiente: Cables de Cobre versus Cables de Fibras Opticas
|
|
|
|